Shepard Tones: repeating tones appear to continuously ascend or descend

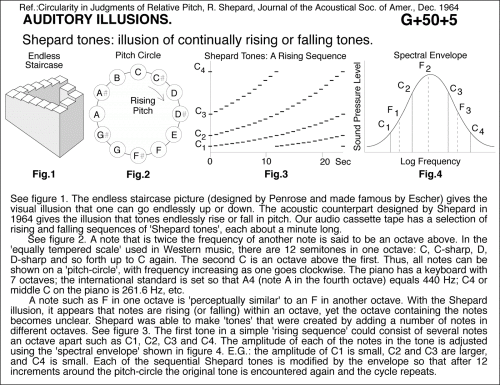
Shepard tones: illusion of continually rising or falling tones. See figure 1. The endless staircase picture (designed by Penrose and made famous by Escher) gives the visual illusion that one can go endlessly up or down. The acoustic counterpart designed by Shepard in 1964 gives the illusion that tones endlessly rise or fall in pitch. Our audio cassette tape has a selection of rising and falling sequences of 'Shepard tones', each about a minute long. See figure 2. A note that is twice the frequency of another note is said to be an octave above. In the 'equally tempered scale' used in Western music, there are 12 semitones in one octave: C, C-sharp, D, D-sharp and so forth up to C again. The second C is an octave above the first. Thus, all notes can be shown on a 'pitch-circle', with frequency increasing as one goes clockwise. The piano has a keyboard with 7 octaves; the international standard is set so that A4 (note A in the fourth octave) equals 440 Hz; C4 or middle C on the piano is 261.6 Hz, etc. A note such as F in one octave is 'perceptually similar' to an F in another octave. With the Shepard illusion, it appears that notes are rising (or falling) within an octave, yet the octave containing the notes becomes unclear. Shepard was able to make 'tones' that were created by adding a number of notes in different octaves. See figure 3. The first tone in a simple 'rising sequence' could consist of several notes an octave apart such as C1, C2, C3 and C4. The amplitude of each of the notes in the tone is adjusted using the 'spectral envelope' shown in figure 4. E.G.: the amplitude of C1 is small, C2 and C3 are larger, and C4 is small. Each of the sequential Shepard tones is modified by the envelope so that after 12 increments around the pitch-circle the original tone is encountered again and the cycle repeats. Ref.:Circularity in Judgments of Relative Pitch, R. Shepard, Journal of the Acoustical Soc. of Amer., Dec. 1964