Plank oscillates on oppositely rotating bicycle wheels.
Primary tabs
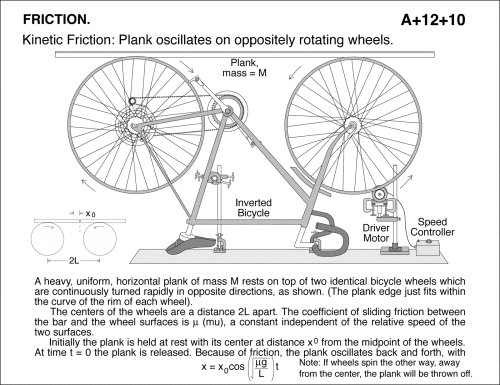
Kinetic Friction: Plank oscillates on oppositely rotating wheels. A heavy, uniform, horizontal plank of mass M rests on top of two identical bicycle wheels which are continuously turned rapidly in opposite directions, as shown. (The plank edge just fits within the curve of the rim of each wheel). The centers of the wheels are a distance 2L apart. The coefficient of sliding friction between the bar and the wheel surfaces is 'mu', a constant independent of the relative speed of the two surfaces. Initially the plank is held at rest with its center at distance x from the midpoint of the wheels. At time t = 0 the plank is released. Because of friction, the plank oscillates back and forth, with x = x.cos((mug/L)^(1/2)) If wheels spin the other way, away from the center, the plank will be thrown off.
UCB Index:
A+12+10
UCB Taxonomy:
Video:
Popularity:
- Log in to post comments