Equal path lengths ball race.

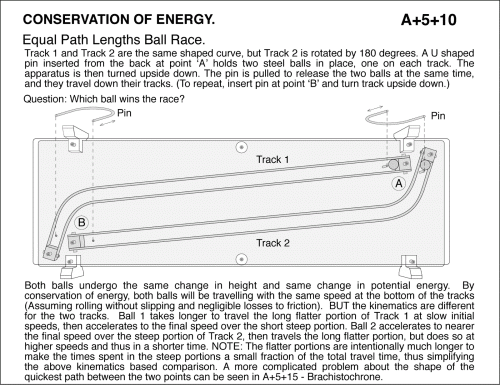
Equal Path Lengths Ball Race. Track 1 and Track 2 are the same shaped curve, but Track 2 is rotated by 180 degrees. A U shaped pin inserted from the back at point A holds two steel balls in place, one on each track. The apparatus is then turned upside down. The pin is pulled to release the two balls at the same time, and they travel down their tracks. (To repeat, insert pin at point B and turn track upside down.) Both balls undergo the same change in height and same change in potential energy. By conservation of energy, both balls will be travelling with the same speed at the bottom of the tracks (Assuming rolling without slipping and negligible losses to friction). BUT the kinematics are different for the two tracks. Ball 1 takes longer to travel the long flatter portion of Track 1 at slow initial speeds, then accelerates to the final speed over the short steep portion. Ball 2 accelerates to nearer the final speed over the steep portion of Track 2, then travels the long flatter portion, but does so at higher speeds and thus in a shorter time. NOTE: The flatter portions are intentionally much longer to make the times spent in the steep portions a small fraction of the total travel time, thus simplifying the above kinematics based comparison. A more complicated problem about the shape of the quickest path between the two points can be seen in