Caruga horn: Varigated tube to blow through

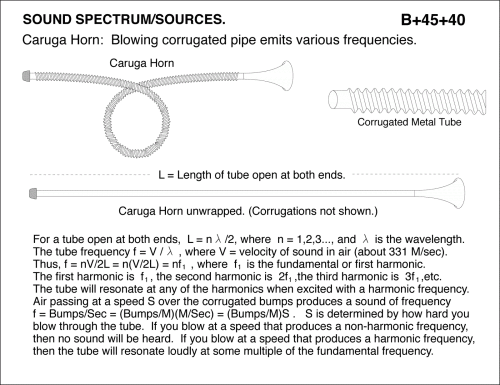
Caruga Horn: Blowing corrugated pipe emits various frequencies. For a tube open at both ends, L = n /2, where n = 1,2,3..., and is the wavelength. The tube frequency f = V / , where V = velocity of sound in air (about 331 M/sec). Thus, f = nV/2L = n(V/2L) = nf , where f is the fundamental or first harmonic. The first harmonic is f , the second harmonic is 2f ,the third harmonic is 3f ,etc. The tube will resonate at any of the harmonics when excited with a harmonic frequency. Air passing at a speed S over the corrugated bumps produces a sound of frequency f = Bumps/Sec = (Bumps/M)(M/Sec) = (Bumps/M)S . S is determined by how hard you blow through the tube. If you blow at a speed that produces a non-harmonic frequency, then no sound will be heard. If you blow at a speed that produces a harmonic frequency, then the tube will resonate loudly at some multiple of the fundamental frequency.